Parallelism with Fine-Grained Streams (Part 2)
While it is possible to process a data set using a large number of parallel streams, a higher degree of parallelism may not be necessarily optimal or even possible. This article explores how to think about parallelism, and discusses many bottlenecks that limit the level of parallelism. It also highlights the need to perform measurements in the target setup due to many factors that cannot be easily quantified.
This article is a sequel to the the blog post Processing Large Data Sets in Fine-Grained Parallel Streams and tutorial Splitting Large Data Sets for Parallel Processing of Queries, in which we discussed how large data sets can be efficiently divided into an arbitrary number of splits for processing across multiple workers in order to achieve high throughput through parallel processing of partition streams.
Query Computation Graph
Let's look at a query in isolation, and how it is processed in parallel. For a given query, the platform’s query planner defines a plan, depicted as a computation graph in the following diagram, for how the query will be executed. In the query computation graph, nodes are workers and edges are data streams.
Please refer to the prior post for the context and terminology.
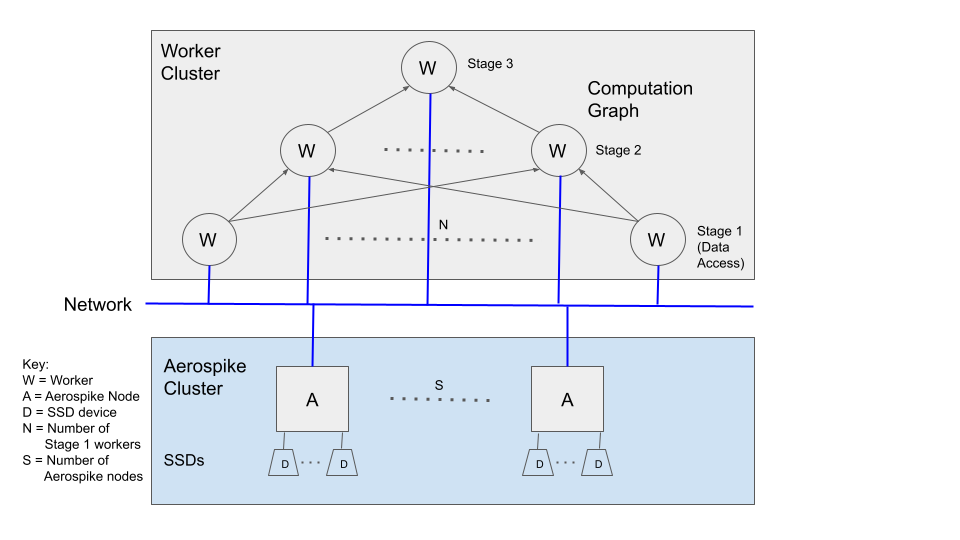
The plan can consist of multiple stages, each stage having a set of workers processing part of the data, and feeding into the next stage. The first stage typically is data access from the appropriate data source(s), and the last stage involves final processing of results such as sort order and size limit.
For example, an aggregate computation on a data set may involve two stages of map-reduce, where the first-stage workers retrieve and process their respective data partitions, and the second-stage aggregates results from the first stage. In a join of data from two sources, the first stage may involve workers retrieving filtered and projected data from the two sources, bucketing data for the next stage based on the join predicate, and forwarding respective buckets to next stage workers to perform the join.
The terms upstream and downstream refer to the direction of data flow through the query graph.
For simplicity, we will focus on the first stage, which is the data access stage.
Data Access Stage
In this stage, the Aerospike data is divided into multiple splits, each accessed and processed by a worker. The data access involves “pushing down” certain operations to the Aerospike cluster in order to minimize data transfer. Such operations include:
Filtering: A subset of records are selected based on some condition. Appropriate indexes are used to evaluate the condition.
Projection: A subset of bins (columns) of each record are selected.
Each worker retrieves and processes records, and forwards results to the next stage. The processing complexity will determine the worker throughput: A simple aggregation can yield a high throughput rate of thousands of records per second whereas a complex transformation involving a database lookup can be much slower yielding just a few tens or hundreds of records per second.
Optimal Parallelism: Matched Stage Throughputs
Parallelism in each stage is defined by the number of workers in that stage.
The throughput of the overall computation is dictated by the slowest stage, or the bottleneck. For maximum efficiency, throughputs of all stages should match to avoid idle resources and/or excessive buffering. In other words, the output throughput of any stage should equal the processing capacity of the following stage.
The throughput of a stage depends on:
worker throughput, which is determined by the computational complexity of processing in that stage, and
number of workers.
The optimizer determines the optimal throughputs at each stage based on the resource requirements of processing in the stage, available resources, and other scheduling constraints. The number of workers at each stage are determined to deliver the matched throughput.
To simplify the discussion, we will focus on the data access stage.
Methodology
The following methodology involves first understanding the resource limitations that will cap the throughput. These are typically disk and network bandwidth, and the number and capacity of the cluster nodes. We use a simple data access request, such as a single scan or a query, to make the discussion concrete. After you calculate the hardware bottleneck and the throughput limit, you may need to further adjustment to the device I/O, network bandwidth, and/or cluster resources. With a given hardware configuration, we can then focus on optimizing software config and request parameters.
Limits and Bottlenecks
The overall throughput is constrained by the following factors:
Device I/O bandwidth: Disk I/O is a common bottleneck in databases. Aerospike uses SSD devices as high-density fast storage.
Database node resources for pushdown processing: Processing such as filtering, bin projection, and UDF execution cannot exceed the available node resources.
Network bandwidth: The data transfer between the server and worker nodes can not exceed the network bandwidth.
Worker resources: The number of workers as well as processing at worker nodes must be within the available capacity.
Let us assume the following parameters in the system:
Number of database nodes: S
Number of workers in data access stage:: N
Device I/O bandwidth at a database node: d
Effective network bandwidth: B
Record size: R
Filter selectivity (fraction of the total records selected): F
Projection factor (reduction in record size due to bin projection): P
Workers per worker node: 100
SSD Throughput
The maximum record I/O throughput at an Aerospike node is d/R. The maximum cumulative record I/O in the cluster is Sxd/R.
Example
An SSD on an AWS instance may have an I/O rating of several GBps (say, 4GBps). Assuming a record size of a few KB (say, 2KB), this translates into several million records per second.
Node SSD I/O = 4x10^9 / (2x10^3) = 2x10^6 or 2 million records per second
Also, assuming a cluster size S=10, a cluster can provide device I/O of several tens of millions of records per second.
Cluster SSD I/O = 10 x 2x10^6 = 20x10^6 or 20 million records per second
If a worker on average can process ten thousand records per second (W=10x10^3), it will take several thousand workers in the data access stage to saturate the disk I/O in such a system.
Max workers in data access stage = 20x10^6 / (10x10^3) = 2x10^3 or 2000 workers.
A lower processing throughput per worker would require a larger number of workers before SSD I/O becomes the bottleneck. Another resource may impose a lower limit on the number of workers.
Server Node Throughput
Each Aerospike node reads records from the disk and outputs processed records for the data access workers to consume. Depending on the type of processing, the number and size of the output records will be different. For example, filtering will reduce the number of records, and bin (column) projections will reduce the size of records.
A query involving a scan with a filter needs to read all records from the device, whereas a secondary-index query needs to read only the records filtered by the secondary index. So:
The max record throughput at an Aerospike node is d/R. This corresponds to the record throughput for a scan without a filter.
The max node record throughput for a scan with filter: d/(RxF)
The max node record throughput for a secondary-index query: d/R
Example
Assuming d, R, and S are the same as above, we have a cluster throughput of several tens of millions of records for a scan query without filtering.
Cluster unfiltered scan throughput = Sxd/R = 10 x 4x10^9 / 2X10^3 = 20X10^6 or 20 million records per second
Assuming selectivity factor F=10, a cluster can provide several millions of records throughput for filtered scans and several tens of millions of records for a secondary-index query.
Cluster filtered scan throughput = Sxd/(RxF) = 10 x 4x10^9 / (2x10^3 x 10) = 2x10^6 or 2 million records per second
Cluster secondary-index query throughput = Sxd/R = 10 x 4x10^9 / (2x10^3 ) = 20x10^6 or 20 million records per second
To saturate the Aerospike cluster throughput in this setup, assuming a processing rate of ten thousand records per second at each worker (W=10^4), it will take thousands of workers for a scan query without filtering as well as a secondary-index query, and hundreds of workers for a scan with filtering.
Max workers for an unfiltered scan = 20x10^6 / (10x10^3) = 2x10^3 or 2000 workers.
Max workers for a filtered scan = 2x10^6 / (10x10^3) = 2x10^2 or 200 workers.
Max workers for a secondary-index query = 20x10^6 / (10x10^3) = 2x10^3 or 2000 workers.
Again, a lower processing throughput per worker would require a larger number of workers before Aerospike cluster throughput becomes the bottleneck. Also, another resource may impose a lower limit on the number of workers.
Complex Pushdown Processing
An aggregation performed on a server node can dramatically reduce the number of result records, typically to just one, and therefore aggregation processing on a server node is not pertinent to the number of workers discussion. Only one or a very few downstream workers would suffice, and we will ignore this case for this discussion. In order to perform complex cluster operations such as aggregations, the number of nodes in the Aerospike cluster, as well as each node’s memory and CPU resources, should be sized appropriately.
We will assume Aerospike node CPU and memory are not a bottleneck for this discussion.
Network Bandwidth
The network I/O at a worker or a server node has an upper limit. For a large worker cluster, the cumulative worker I/O can exceed the subnet bandwidth. Additionally, the traffic to the database may need to traverse routers and gateways which will also impose their own limits. The most stringent of these limits can become the bottleneck.
Example
In AWS, the network I/O limit for an instance may range from a few Gbps to 100s of Gbps per instance. A cluster on a subnet may have a total network capacity of 100’s of Gbps for all nodes. If the Aerospike cluster placement requires access to another VPC in AWS, the VPC Gateway I/O limit is in the range of 100 Gbps.
We can reasonably work with the effective network bandwidth limit (B) of 100 Gbps.
Compare this to the Aerospike cluster SSD throughput of several tens of GBps or hundreds of Gbps, and note that the network bandwidth is smaller of the two, potentially an order of magnitude smaller. In such a system, the network bandwidth can become the bottleneck.
Assuming a maximum bandwidth of 100 Gbps and using the prior values for R and W, we will need several hundred workers to saturate the network.
Max workers to saturate network I/O = B / (WxR) = 100/8 x 10^9 / (W*R) = 12.5x10^9 / (10^4 x 2x10^3) = 6.25 x 10^2 = 625
Interestingly, for a scan with filtering and projection, the network bandwidth requirement at data access stage reduces by a factor or FxP because now fewer records of smaller size need to traverse the network. Assuming F=10 and P=10, the network bandwidth needed just for the data access portion goes down by a hundred fold, which can shift the bottleneck to the SSD I/O. Removing the SSD I/O bottleneck may entail adding additional SSD drives to each Aerospike node.
Worker Nodes
The number of available worker nodes can itself be the limit. A worker node can run a large number of worker processes (or workers), typically configured at 1-2 times the number of CPU cores.
Example
If we assume 100 workers per worker node, the number of data access worker nodes needed:
To saturate the cluster record throughput the number of worker nodes is up to a few tens.
Worker nodes = Range of workers / workers per worker node = Hundreds to thousands / 100 = a few to tens of nodes
To saturate the effective network bandwidth the number of worker nodes is in single digits.
Worker nodes = Range of workers in hundreds / 100 = a few nodes
A processing throughput per worker lower than ten thousand records per second as assumed above would mean a larger number of worker nodes to hit the bottleneck (which is the network bandwidth in this case). Note, the above gives the nodes needed in the data access stage only, and not in the entire worker cluster.
Concurrent Jobs
Concurrent computations on the worker cluster share the resources and throughput.
Example
If a shared platform requires fair scheduling of, say, 3 similar computations at a time, the resource limit for each computation will be 1/3 of the total available limits. Each query in our scenario, thus, can only need a few worker nodes or a few hundred workers before reaching the bottleneck, which is the network bandwidth in our example.
Another Setup
Let's run through a lower tier hardware setup for a similar workload of scans and queries:
Number of database nodes: S = 3
Device I/O bandwidth at a database node: d = 2 GBps
Effective network bandwidth: B = 50 Gbps
Workers per worker node: 50
Record size: R = 2KB
Filter selectivity : F = 10
Projection factor : P = 10
Device I/O limit
Cluster SSD I/O = Sxd/R = 3 x 2x10^9/2x10^3 = 3 x 10^6 or 3 million records per second
Max workers in data access stage = 3x10^6 / (5x10^2) = 6 x 10^3 or 6000 workers.
Database throughput limit
Cluster unfiltered scan throughput = Sxd/R = 3 x 2x10^9 / 2x10^3 = 3x10^6 or 3 million records per second
Max workers for unfiltered scan = 3x10^6 / (10^3) = 3x10^3 or 3000 workers.
Cluster filtered scan throughput = Sxd/(RxF) = 3 x 2x10^9 / (2x10^3 x 10) = 3x10^5 or 0.3 million records per second
Max workers for filtered scan = 0.3x10^6 / (10^3) = 0.3x10^3 or 300 workers.
Cluster secondary-index query throughput = Sxd/R = 3 x 2x10^9 / (2x10^3 ) = 3x10^6 or 3 million records per second
Max workers for secondary-index query = 3x10^6 / (10^3) = 3x10^3 or 3000 workers.
To saturate the cluster record throughput the number of worker nodes is in low tens.
Range of workers / workers per worker node = 300-3000 / 50 -> 6 - 60 nodes
Network bandwidth limit
Max workers to saturate network I/O = B/(WxR) = 50/8 x 10^9 / (WxR) = 6.25x10^9 / (10^3 x 2x10^3) = 3.125 x 10^3 = 3125 workers
To saturate the effective network bandwidth the number of worker nodes is in low tens.
Workers / workers per worker node = 3125 / 50 -> 62.5 nodes
Concurrency limit
With 3 similar computations at a time, the resource limit for each computation will be 1/3 of the total available limits, or up to 21 worker nodes.
Optimizing Data Access
The problem of optimizing data access is to achieve performance and throughput as close to the hardware limits as possible.
In general, streamlined processing with fewest context switches provides superior efficiency. So data access is likely to be more efficient and provide better throughput where:
data is spread across fewer server nodes as it requires less split-merge overhead,
access chunk (or page) size is larger as it allows longer uninterrupted runs, and
asynchronous mode is used as resources are not held up while waiting on response.
At the same time, there are many factors that cannot be easily predicted. Concurrency conflicts, context switching, and flow control delays can lead to potential bottlenecks. Suboptimal system configuration such as missing indexes, and suboptimal choice of the query plan due to incorrect heuristics or metadata will also lead to througput surprises. Therefore, the best way to find out the optimal parameters is to experiment in the target environment with the target workload.
The hardware capacities of a given environment will limit the level of parallelism and throughput. Different workloads place different types of resource burden and can expose bottlenecks in different areas. The system should be balanced with the desired workload in mind so that a bottleneck in one area does not waste unused capacity in other areas. While a good understanding of such limits is important, there are many factors that are dynamic and cannot be predicted easily. Therefore, experimenting in the target environment is essential to discover the system model for optimal performance.




